Familywise Error Rates > Holm-Bonferroni Method

You may want to read this article first: Familywise Error Rates.

What is the Holm-Bonferroni Method?

The Holm-Bonferroni Method (also called Holm’s Sequential Bonferroni Procedure) is a way to deal with familywise error rates (FWER) for multiple hypothesis tests. It is a modification of the Bonferroni correction. The Bonferroni correction reduces the possibility of getting a statistically significant result (i.e. a Type I error) when performing multiple tests. Although the Bonferroni is simple to calculate, it suffers from a lack of statistical power. The Holm-Bonferroni method is also fairly simple to calculate, but it is more powerful than the single-step Bonferroni.

Formula

The formula to calculate the Holm-Bonferroni is:
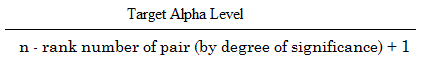Image Added

Where:

• Target alpha level = overall alpha level (usually .05),
• n = number of tests.

This next example shows how the formula works.

Example

Question: Use the Holm-Bonferroni method to test the following four hypotheses and their associated p-values at an alpha level of .05:

• H₁ = 0.01.
• H₂ = 0.04
• H₃ = 0.03
• H₄ = 0.005

Note: we already know the p-values associated with each hypothesis. If you don’t know the p-values, run a test for each hypothesis before attempting to adjust FWER using the Holm-Bonferroni method.

Step 1: Order the p-values from smallest to greatest:

• H₄ = 0.005
• H₁ = 0.01
• H₃ = 0.03
• H₂ = 0.04

Step 2: Work the Holm-Bonferroni formula for the first rank:
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

Step 3: Compare the first-ranked (smallest) p-value from Step 1 to the alpha level calculated in Step 2:
Smallest p-value, in Step 1 (H₄ = 0.005) < Alpha level in Step 2 (.125).
If the p-value is smaller, reject the null hypothesis for this individual test.

The p-value of .005 is less than .125, so the null hypothesis for H₄ is rejected.

Step 4: Repeat the HB formula for the second rank .
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167

Step 5: Compare the result from the HB formula in Step 4 to the second-ranked p-value: 
Second ranked p-value, in Step 1 (H₁ = 0.01) < Alpha level in Step 2 (.0167).
The p-value of .01 is less than .0167, so the null hypothesis for H₁ is rejected as well.

Step 6: Repeat the HB formula for the third rank.
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025

Step 7: Compare the result from the HB formula in Step 6 to the third-ranked p-value: 
Third ranked p-value, in Step 1 (H₃ = 0.03) > Alpha level in Step 6 (.025).
The p-value of .03 is greater than .025, so the null hypothesis for H₃ is not rejected.

The testing stops when you reach the first non-rejected hypothesis. All subsequent hypotheses are non-significant (i.e. not rejected).

Reference:
Holm, S. 1979. A simple sequential rejective multiple test procedure. Scandinavian Journal of Statistics 6:65-70