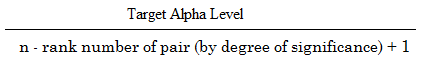Bonferroni

FDR

Holm-Bonferroni

Holm-Bonferroni Method: Step by Step

Familywise Error Rates > Holm-Bonferroni Method

You may want to read this article first: Familywise Error Rates.

What is the Holm-Bonferroni Method?

The Holm-Bonferroni Method (also called Holm’s Sequential Bonferroni Procedure) is a way to deal with familywise error rates (FWER) for multiple hypothesis tests. It is a modification of the Bonferroni correction. The Bonferroni correction reduces the possibility of getting a statistically significant result (i.e. a Type I error) when performing multiple tests. Although the Bonferroni is simple to calculate, it suffers from a lack of statistical power. The Holm-Bonferroni method is also fairly simple to calculate, but it is more powerful than the single-step Bonferroni.

Holm-Bonferroni Method: Step by Step

Familywise Error Rates > Holm-Bonferroni Method

You may want to read this article first: Familywise Error Rates.

What is the Holm-Bonferroni Method?

The Holm-Bonferroni Method (also called Holm’s Sequential Bonferroni Procedure) is a way to deal with familywise error rates (FWER) for multiple hypothesis tests. It is a modification of the Bonferroni correction. The Bonferroni correction reduces the possibility of getting a statistically significant result (i.e. a Type I error) when performing multiple tests. Although the Bonferroni is simple to calculate, it suffers from a lack of statistical power. The Holm-Bonferroni method is also fairly simple to calculate, but it is more powerful than the single-step Bonferroni.

Formula

The formula to calculate the Holm-Bonferroni is:


Where:

• Target alpha level = overall alpha level (usually .05),
• n = number of tests.

This next example shows how the formula works.

Example

Question: Use the Holm-Bonferroni method to test the following four hypotheses and their associated p-values at an alpha level of .05:

• H₁ = 0.01.
• H₂ = 0.04
• H₃ = 0.03
• H₄ = 0.005

Note: we already know the p-values associated with each hypothesis. If you don’t know the p-values, run a test for each hypothesis before attempting to adjust FWER using the Holm-Bonferroni method.

Step 1: Order the p-values from smallest to greatest:

• H₄ = 0.005
• H₁ = 0.01
• H₃ = 0.03
• H₂ = 0.04

Step 2: Work the Holm-Bonferroni formula for the first rank:
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

Step 3: Compare the first-ranked (smallest) p-value from Step 1 to the alpha level calculated in Step 2:
Smallest p-value, in Step 1 (H₄ = 0.005) < Alpha level in Step 2 (.125).
If the p-value is smaller, reject the null hypothesis for this individual test.

The p-value of .005 is less than .125, so the null hypothesis for H₄ is rejected.

Step 4: Repeat the HB formula for the second rank .
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167

Step 5: Compare the result from the HB formula in Step 4 to the second-ranked p-value: 
Second ranked p-value, in Step 1 (H₁ = 0.01) < Alpha level in Step 2 (.0167).
The p-value of .01 is less than .0167, so the null hypothesis for H₁ is rejected as well.

Step 6: Repeat the HB formula for the third rank.
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025

Step 7: Compare the result from the HB formula in Step 6 to the third-ranked p-value: 
Third ranked p-value, in Step 1 (H₃ = 0.03) > Alpha level in Step 6 (.025).
The p-value of .03 is greater than .025, so the null hypothesis for H₃ is not rejected.

The testing stops when you reach the first non-rejected hypothesis. All subsequent hypotheses are non-significant (i.e. not rejected).

Reference:
Holm, S. 1979. A simple sequential rejective multiple test procedure. Scandinavian Journal of Statistics 6:65-70
Holm-Bonferroni Method: Step by Step was last modified: February 2nd, 2017 by Andale
By Andale | September 18, 2016 | Statistics How To | 2 Comments |

Sidak

If you run kk independent statistical tests using αα as your significance level, and the null obtains in every case, whether or not you will find 'significance' is simply a draw from a random variable. Specifically, it is taken from a binomial distribution with p=αp=α and n=kn=k. For example, if you plan to run 3 tests using α=.05α=.05, and (unbeknownst to you) there is actually no difference in each case, then there is a 5% chance of finding a significant result in each test. In this way, the type I error rate is held to αα for the tests individually, but across the set of 3 tests the long-run type I error rate will be higher. If you believe that it is meaningful to group / think of these 3 tests together, then you may want to hold the type I error rate at αα for the set as a whole, rather than just individually. How should you go about this? There are two approaches that center on shifting from the original αα(i.e., αoαo) to a new value (i.e., αnewαnew):

Bonferroni: adjust the αα used to assess 'significance' such that

αnew=αokαnew=αok

Dunn-Sidak: adjust αα using

αnew=1−(1−αo)1/kαnew=1−(1−αo)1/k

(Note that the Dunn-Sidak assumes all the tests within the set are independent of each other and could yield familywise type I error inflation if that assumption does not hold.)

It is important to note that when conducting tests, there are two kinds of errors that you want to avoid, type I (i.e., saying there is a difference when there isn't one) and type II (i.e., saying there isn't a difference when there actually is). Typically, when people discuss this topic, they only discuss—and seem to only be aware of / concerned with—type I errors. In addition, people often neglect to mention that the calculated error rate will only hold if all nulls are true. It is trivially obvious that you cannot make a type I error if the null hypothesis is false, but it is important to hold that fact explicitly in mind when discussing this issue.

I bring this up because there are implications of these facts that appear to often go unconsidered. First, if k>1k>1, the Dunn-Sidak approach will offer higher power (although the difference can be quite tiny with small kk) and so should always be preferred (when applicable). Second, a 'step-down'approach should be used. That is, test the biggest effect first; if you are convinced that the null does not obtain in that case, then the maximum possible number of type I errors is k−1k−1, so the next test should be adjusted accordingly, and so on. (This often makes people uncomfortable and looks like fishing, but it is not fishing, as the tests are independent, and you intended to conduct them before you ever saw the data. This is just a way of adjusting αα optimally.)

The above holds no matter how you you value type I relative to type II errors. However, a-priorithere is no reason to believe that type I errors are worse than type II (despite the fact that everyone seems to assume so). Instead, this is a decision that must be made by the researcher, and must be specific to that situation. Personally, if I am running theoretically-suggested, a-priori, orthogonal contrasts, I don't usually adjust αα.

(And to state this again, because it's important, all of the above assumes that the tests are independent. If the contrasts are not independent, such as when several treatments are each being compared to the same control, a different approach than αα adjustment, such as Dunnett's test, should be used.)